符号与机器(五):重新发明 Lambda 演算
问题:给出一个系统,能够自动判定 1 + 1 = 2。
今天我们试着通过这个判定问题,来重新发明一遍 Lambda 演算。🚗
首先,直觉上,很容易想到,给出一个苹果数数系统,很容易得出1个加上1个苹果,确实是2个苹果。
🍎 + 🍎 = 🍎 🍎
但是这个系统满足问题的条件吗?答案是否定的。因为这不是一个自动判定的系统,中间需要人脑的协助来判定,无法自动推演判定。
延伸问题:算盘是图灵完备的吗?
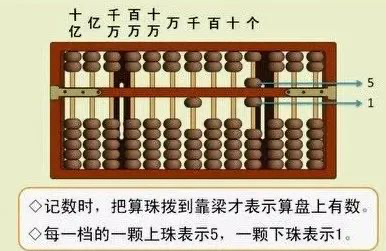
算盘同样属于数数系统,只是通过算珠来表示不同的数字,所以算盘 🧮 和苹果 🍎 其实是等价的。都不是通用的计算系统,也就是说不是图灵完备的。
继续,回到问题本身,我们需要一套符号系统来表示 1、2、+,并且这些符号能够通过某些规则自动运算。那么,如何表示任意的数字,而且支持自动判定呢?
让我们回到自然数的定义本身:
- 0 是自然数
- 每一个自然数的后继也是自然数
我们尝试给出如下符号表示规则:
0 = z
后继 = s
1 = s 0 = s z
2 = s 1 = s s 0 = s s z
3 = s 2 = s s 1 = s s s 0 = s s s z
通过不停地增加后继 s,我们能够得到所有自然数的定义。这其实就是一种不断增加 s 的变换操作,其中 s 和 z 可以是任意符号参数。所以我们选择数学中的函数作为基础组件,将数字的操作和表示形式重新定义如下:
0 = lambda s z . z
后继 = lambda s z . s
后继变换 f = lambda x s z . s (x s z)
1 = (f 0)
= (lambda x s z . s (x s z)) 0
= lambda s z . s (((lambda s z . z) s z))
= lambda s z . s z
2 = (f 1)
= lambda s z . s (s z)
3 = (f 2)
= lambda s z . s (s (s z))
可以发现,其实我们上面定义的,就是丘奇数!!
继续,有了上面自然数以及变换的定义,再来看看,在我们给出的判定系统以及规则中,如何定义加法+。
关于加法的算法描述:
1 + 1 = ((lambda x y . x + y) 1 1)
= ((lambda x y s z. x s (y s z)) 1 1)
= (lambda y s z . (lambda s z . s z) s (y s z) 1)
= (lambda y s z . s (y s z) ) 1
= lambda s z . s ((lambda s z . s z) s z)
= lambda s z . s (s z)
= 2
结论:1 + 1 = 2,即 1 + 1 和 2 是等价的。
对上面的判定系统的进行提炼和抽象,我们可得到:
- 函数表达式定义形式,其中 x 表示函数参数,body 表示函数表达式
lambda x . body
- 函数表达式通过参数传递来求值,比如:
(lambda x . x) y = y
- 自由绑定和绑定变量
lambda x . + x y
上面函数表达式中,+ 和 y 是自由变量,因为没有出现在函数表达式的输入参数列表中。x 出现在了输入参数列表中,所以是绑定变量。
- 两个应用规则
- Alpha 变换
lambda x . x = lambda y . y
Alpha 变换就是参数名变换操作,比如上面的两个表达式,是等价的。就说,如果参数名称变了,并且 body 中对应的参数也替换成了相应的名称,对函数表达式的结果无影响。
- Beta 规约
(lambda x . x)(lambda y . y) = (lambda y . y)
Beta 规约就是将输入变量,绑定到函数表达式的 body 中,也就是函数求值。比如上面的表达式,我们将 x 替换成 lambda y . y 得到 lambda y . y,这就是一个规约过的函数表达式。这两个表达式也是等价的。
就这样,我们重新发明了 Lambda 演算!!